Longitud de arco

Oscar Enrique Gonzalez López

Clase del 26 de Octubre 2024

Profe. Alejandro Gómez

Tema: Longitud de arco

 

Lo aprendido en clase:

Lo que aprendí en clase fue longitud de arco.  Se me ha complica mucho todo el procedimiento hasta llegar a integrar, pero reforzare mas del tema. 

Conocimiento Consultado:

Longitud de Arco de la Curva y = f (x)

En aplicaciones anteriores de integración, requeríamos quef(x)$𝑓(𝑥)$ la función fuera integrable, o como mucho continua. Sin embargo, para calcular la longitud del arco tenemos un requisito más estricto paraf(x)$𝑓(𝑥)$. Aquí, requerimosf(x)$𝑓(𝑥)$ ser diferenciables, y además requerimos que su derivado,f'(x),$𝑓\prime (𝑥),$ sea continuo. Funciones como esta, que tienen derivadas continuas, se llaman lisas. (Esta propiedad vuelve a aparecer en capítulos posteriores.)

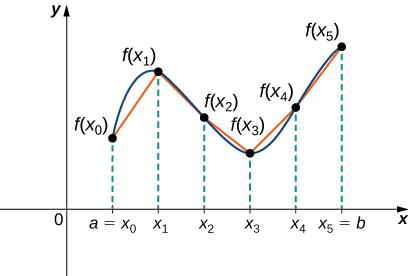
Dejarf(x)$𝑓(𝑥)$ ser una función suave definida sobre[a,b]$[𝑎,𝑏]$. Queremos calcular la longitud de la curva desde el punto(a,f(a))$(𝑎,𝑓(𝑎))$ hasta el punto(b,f(b))$(𝑏,𝑓(𝑏))$. Comenzamos usando segmentos de línea para aproximar la longitud de la curva. Parai=0,1,2,…,n$𝑖=0,1,2,\dots ,𝑛$, dejarP=xi$𝑃={𝑥}_{𝑖}$ ser una partición regular de[a,b]$[𝑎,𝑏]$. Después, parai=1,2,…,n$𝑖=1,2,\dots ,𝑛$, construya un segmento de línea desde el punto(xi−1,f(xi−1))$({𝑥}_{𝑖-1},𝑓({𝑥}_{𝑖-1}))$ hasta el punto(xi,f(xi))$({𝑥}_{𝑖},𝑓({𝑥}_{𝑖}))$. Aunque pueda parecer lógico usar segmentos de línea horizontales o verticales, queremos que nuestros segmentos de línea se aproximen lo más posible a la curva. La figura6.4.1$\mathrm{6.4.}1$ representa este constructo paran=5$𝑛=5$.

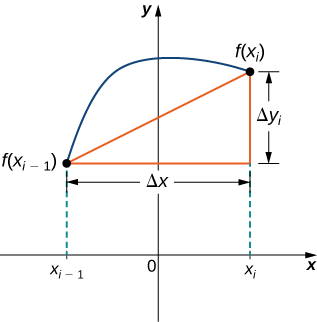
Para ayudarnos a encontrar la longitud de cada segmento de línea, observamos el cambio en la distancia vertical así como el cambio en la distancia horizontal en cada intervalo. Debido a que hemos utilizado una partición regular, el cambio en la distancia horizontal sobre cada intervalo viene dado porΔx$\Delta 𝑥$. Sin embargo, el cambio en la distancia vertical varía de un intervalo a otro, por lo que usamosΔyi=f(xi)−f(xi−1)$\Delta {𝑦}_{𝑖}=𝑓({𝑥}_{𝑖})-𝑓({𝑥}_{𝑖-1})$ para representar el cambio en la distancia vertical a lo largo del intervalo[xi−1,xi]$[{𝑥}_{𝑖-1},{𝑥}_{𝑖}]$, como se muestra en la Figura6.4.2$\mathrm{6.4.}2$. Tenga en cuenta que algunos (o todos)Δyi$\Delta {𝑦}_{𝑖}$ pueden ser negativos.

Video relacionado al tema:

Imagen:

Referencias:

https://espanol.libretexts.org/Matematicas/Libro%3A_Calculo_(OpenStax)/06%3A_Aplicaciones_de_Integraci%C3%B3n/6.04%3A_Longitud_de_Arco_de_una_Curva_y_%C3%81rea_de_Superficie